画像のボケの具合を表すのが、点広がり関数と線広がり関数です。
ですが、私自身この二つの内容について大学の授業で学んだ覚えもないほど、印象に残っていませんでした。
同じように感じている方はどの程度いるのか、わかりませんが、今回はこの二つについてまとめてみたいと思います。
スポンサーリンク
広がり関数とは?
点広がり関数と線広がり関数といいましたが、そもそも、この二つに共通する『広がり関数』とはどういったことを表す言葉なのでしょうか。
広がり関数とは、X線画像が出来上がるまでに起こるボケによって、小さい点であれ、ボンヤリと広がりを持った分布になることです。
どういうことか。
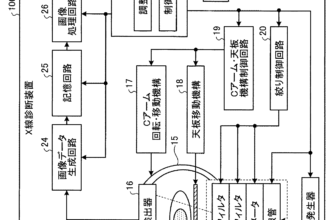
X線画像とは、X線が検出器と呼ばれるフィルムに入射し、その信号を画像を作成するシステムで読み取り、出力することで出来上がります。
が、しかし、X線によって入力された信号は画像の作成システムを経過するごとにぼやけてしまうのです。
テレビの企画でもなんでもいいですが、絵の行う伝達ゲームのようなものを想像できますでしょうか。最初にお題を与えられ、そのお題の絵を描き、それを次の人に伝え、伝えられた人はその絵を参考にまた自分で絵を描き、また次の人へと伝え、最後の人がにお題が何だったのか答えるゲームのことです。
このゲームの面白さは、与えられたお題を忠実に絵に描いて次の人に伝えたいはずなのに、絵が上手い人や下手な人、または特徴だけを上手く伝えることが出来る人や、一生懸命に描こうとしすぎて描ききれなかったりと、途中経過の変化と最終的に正解に辿り着けられるのかわからないドキドキです。
一体、何がいいたいのかというと、例え入力される情報が誰もが見てわかるものであっても、それを多くの過程を経ると、情報が足されたり、減らされたりして最終的には正しい情報がボケてしまい、違った情報となってしまうということです。
情報が全く違ってしまうということはありませんが、X線画像でも同様です。
X線の検出器にいかに正確に無駄な情報なく入力されたところで、画像を作るまでには、入射されたX線を光や電子に変換し読み取り、読み取った情報を出力するために、出力システムに再度入力するといったような、入力から出力まで様々なシステムを通過する必要があります。
そして、いくつものシステムを経過する度に情報がボケてしまい、それが画像となって表現されることになるのです。
この画像がボケて、どのような広がりを持ってしまったのかというのを表現する手段が広がり関数なのです。
『ボケないためのシステムを作ればいいのではないか?!』という疑問が生まれるかもしれませんが、現段階ではこれは無理です。企業ごとにボケないための工夫は多くされていますが、どうしてもX線から画像を作る上では、ボケというのは避けられない現象であるといえます。
スポンサーリンク
点広がり関数とは?
では、点広がり関数とはなんなのでしょうか。
これは、X線が点状に検出器に入力され、本来、点として画像に表現されなければならないものが、どの程度広がりを持ち、小さな円のように広がりを持った表現になってしまっているのかを調べることになります。
上でも言いましたが、X線画像を作成する過程では必ず、画像はボケの成分を含んだ状態で表現されます。
そのため、いくら点状にX線が入力されたところで、ボケて点ではなく、小さな円となって表現されてしまうのです。
その点から円にどの程度広がるかは、その画像システムの性能によって異なりそれを調べるのが点広がり関数(point spread funcion:PSF)です。
ただ、点とは2次元的にだけ分布があるため、空間という3次元方向をの評価には向いていないという欠点があるため注意が必要です。
では、空間的なボケの調べるにはどうしたらいいのか。
それが、線広がり関数となります。
線広がり関数とは?
線広がり関数(line spread function:LSF)とは、スリットのように線状にX線が入力され、その線がどの程度広がりをもって画像に出力されるのか、表現したものです。
点のボケを表現した点広がり関数(PSF)と比較し、線広がり関数(LSF)は、ボケの方向性がはっきりとするため、空間的な画像評価によく利用されています。
といっても、線広がり関数とは点広がり関数の積分関係があるため、線広がり関数の一部分を切り取り、表現された広がり関数は点広がり関数ということになります。
なので、線広がり関数は点広がり関数の使って式で表すことも可能であり、以下のような関係をもっていることになります。