ＭＲＩ：Ｋ空間とその埋め方とは？

MRIを学ぶ上で避けられず、かつ、理解しにくい領域の一つがｋ空間です。ｋ空間はMRI特有の空間であり、聞きなれないためにその難しさを助長させているようにも感じます。

しかし、MRIについてｋ空間から理解することで、応用された高速撮像法に関しても、「なぜ速く撮像できるのか？」を理解できるはずです。

今回は、ｋ空間についてまとめてみたいと思います。

ｋ空間とは？

k空間はMRI特有のもので、コンピュータの中に存在しているものです。

では、どんな役割を持った空間なのでしょうか。

ｋ空間とは、装置から検出されたMR信号を書き込み・保管する場所（空間）のことです。

MRIでは、得られる信号が直接的に画像になるわけではありません。被写体から得られる最初の信号は、複雑波と呼ばれるいくつものの波形が重なって出来たものです。また、最終的に画像を作るのに得る複雑波は256個（画素数によって変化しますが・・・）に相当します。

つまり、一枚のMR画像を作るのに、必要な信号数は相当な数に上り、その信号を全部そろわせるための空間が必要になるのです。それがｋ空間です。

そんなｋ空間は、罫線のはいった記録帳に例えると理解しやすくなります。

記録帳はページの真ん中をまたぎ、罫線が元から入っており、1行1行がわかれ整理しやすいものを想像しましょう。実際のMR信号が保存されるｋ空間はマス目のように縦にも横に罫線が入ったものが使用されていますが、まずは横方向（左から右へ）に罫線が絵が描かれた記録帳を想像するだけで十分です。最初から1コマごとに分かれている必要はありせん。

さて、今後の話を理解しやすくするためにひとつだけ重要なことを決めておきたいと思います。

それは、横方向軸を周波数エンコーディングに、垂直軸が位相エンコーディングに相当するということです。

MRIでは周波数方向と位相方向は、任意で決めることが出来るため話がずれないように、これを今回の基本的なルールとしておきます。一応、誤解が生まれないために、図を使って以下に示しておきます。

では、まとめを続けたいと思います。

ｋ空間は受信されたMR信号が保存されていきます。そのｋ空間（記録帳）には、左から右へと水平方向の罫線が引かれており、受信された信号はその行内に記録されていくことになります。（授業の内容をノートの線にそって、綺麗にまとめていくことを想像するとわかりやすいかもしれません。）

この記録帳の1ページ分に相当する信号を得た時にMR画像を作るのに十分な信号を得たことになります。逆に言うと、1ページ分の信号を得るためにそれだけの時間と労力をかける必要があるのです。

その労力とは、傾斜磁場に相当します。

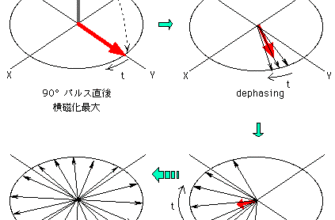
MRでは、傾斜磁場をかけて、スライス面内に含まれる臓器の位置を把握しています。もっと、具体的に言えば、静磁場下にある組織のプロトンは大きな縦磁化となって歳差運動をしています。それを90°パルスなどによって、歳差運動周期が揃えられるので、一時的に組織に含まれるプロトンはみな同じ周期と位相でグルグルとまわっているのです。

しかし、この状態の組織からMR信号を受け取ってしまうと、どこから信号を得たのかというのがあいまいになってしまいます。

そこで使用されるのが傾斜磁場です。周波数エンコーディングと位相エンコーディングによって、周期と位相にズレを起こし、その状態からMR信号を受け取ることで臓器の位置を特定することが可能になり、画像を作ることができます。

ただ、この1枚のMR画像を作るのは、傾斜磁場を労力を一度だけ行えばいいわけではありません。より確実で明確な情報となるために、何度もかけそのすべてのMR信号をｋ空間という保存箱におさめていく必要があるのです。

その回数とは、画素数によって影響を受けます。

MRの画像は画素の行列であり、左から右に向けた行、上から下に向けた列から成り立っていることを思い出しましょう。例えば、256×128の行列であれば、ひとつの行に256画素あり、ひとつの列には128画素あります。

MR画像を作るには、この画素を全て埋める必要があり、埋めるためにMR信号を得るためには傾斜磁場が必要です。

そして、一度の位相エンコーディングで埋めることが可能な画素は、基本的には１行分（左から右への256画素と上から下への1画素のみ）だけに相当します。（高速撮像法を使用していない場合）

よって、256×128のｋ空間が用意されている場合、1枚のMR画像を作るためには、最低でも位相エンコーディングを128回必要とすることになるのです。それだけの時間がかかることになります。

ｋ空間のルールとは？

ｋ空間とは、MR信号を保存する記録帳のようなもんで、その実態は画素行列であることがわかっていただけた後は、ｋ空間に信号を書き込むときのルールを紹介します。

1回の位相エンコーディングによって得られるMR信号はｋ空間の1行分に相当します。実際に得たMR信号をｋ空間に保存していくことになるのですが、この時に特有のルールがあるのです。

それは、まず記録帳の中央行から埋めるというルールです。

それはなぜか。

256×128のMR画像を1枚得るためには、128回の位相エンコーディングが必要になります。しかし、1回目と傾斜磁場と128回目の傾斜磁場とでは、得られるMR信号がその強度が異なるからです。

実際に、得られるMR信号は段々と弱くなっていきます。

位相エンコーディング傾斜磁場はプロトンの間で位相のずれを引き起こします。（組織ごとにある時計が最初は同じ時間を指していても、位相エンコーディングの度にずれてしまい、同じ時間を指すことができなくなってしまうようなもの。）この位相のずれのために、MR信号全体、つまり一定方向を向いた全ての小さな磁化ベクトルの総和は減少してしまっているのです。

位相エンコーディング傾斜磁場が強いほど、位相のずれは大きくなり、全体の信号がより少なりなります。逆もまた然りで、位相エンコーディング傾斜磁場が弱いほど、全体信号は強くなるのです。

ｋ空間を埋めるために、必要な位相エンコーディング傾斜磁場は128回です。位相エンコーディング傾斜磁場をかければかけるほど、組織の位相はずれをおこすため1回目の最も弱い位相エンコーディング傾斜磁場によって得られた1番大きなMR信号を最も重要な中央行に埋めることになるのです。（実際には、位相エンコーディング傾斜磁場の強度も測定ごとに変化している）

真ん中の行を埋め終わった次は、1回目よりも少し強い傾斜磁場を使って、中央行の1段上に書きこまれます。同様に3回目は、2回目よりもまた少し強い位相エンコーディング傾斜磁場を使い、少し減少した信号を得て、先ほど書き込んだ次の上段の行に記録されていきます。

このような手順によって、中央行から上にある全ての行が埋め尽くされるまで、続くのです。上が埋め終わったら、同様に中央から下の行も中央から下に向かって埋めていくことになります。

ただし、中央から上の段を埋めていた時と異なるのは、位相エンコーディング傾斜磁場の向きが反対方向に切り変わっているということです。（傾斜磁場コイルに先ほどとは逆方向から電流を流すことで発生させる）

中央行の下にある行は、弱い位相エンコーディング傾斜磁場を使った信号記録で、さらにその下の行は少し強めの位相エンコーディング傾斜磁場による信号を記録することになります。

1枚のMR画像を作るのに相当な労力と時間が必要なのが想像できるのではないでしょうか。

ｋ空間の埋め方のルールも重要でしたが、もうひとつだけ大事なルールがあります。

それは、ｋ空間に埋められたMR信号には対称性があるということです。

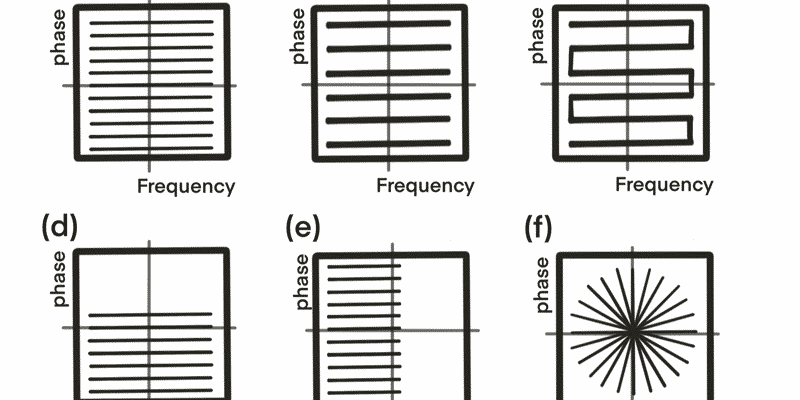
実際に、中央行から上段にある信号と下段にある信号はあたかも鏡像のようになっています。同様に、中央列から左側と右側の信号も鏡像のようになっています。

この対称性はとても重要です。

今回は詳細は省きますが、ｋ空間の下半分のデータが上半分のデータの反対になっているのであれば、必ずしも全ての範囲に渡って測定を行う必要がないということになるからです。

半分だけデータの収集を行い、そのデータを反転させてコピーすればよいのですから。（実際は、半分より少し多めの測定を行いますが・・・）

結果的に撮影時間も短くなります。

データを半分だけフーリエ変換するため、ハーフフーリエ画像法とも呼ばれるらしいですが、この方法を話し始めると長くなるため、またの機会にしたいと思います。

今回は、ここまで理解いただければ幸いです。