MRI：ｋ空間と画像の関係とは？

以前にまとめたｋ空間とはに続き、画像との関係性についてもまとめてみたいと思います。

 

ｋ空間が画像にどう影響し、ｋ空間からどうやって画像が作られているのか理解の助けになれば幸いです。

スポンサーリンク

ｋ空間と画像の関係とは？

ここまでは、ｋ空間がどういったもので、どういうルールがあるのかということをまとめて来ました。

 

ただ、これだけではｋ空間の話は十分ではありません。ｋ空間と画像の関係性も少しだけ知る必要があります。

 

少しだけ復習になりますが、ｋ空間の中央行には最も弱い位相エンコーディング傾斜磁場と使って得られた信号が書き込まれています。その結果、最も強い全体信号が中心行には書き込まれていることになるのです。

 

強い全体信号が発生したということは、この強い全体信号を作っている個々の信号も強いと予想されます。そして、その成分信号が強い場合、その成分信号間の差異がはっきりと表れてくるのです。

 

どういうことか。

 

例えば、海を遠くから想像してみましょう。ある日の海の波はあまり高くなく、遠くから見ると波が立っているのかすら見分けはつかないでしょう。一方、波が高い海の場合、遠くから見ても波が立っていることがわかり、船に乗るのも危険なほどです。つまり、波が大きくうねるようであれば、その差はわかりやすいですが、反対に波が小さければ、近くに行かなければ、波の高さの差がわかりにくい状態であるといえます。

 

これをMR画像に置き換えてみると、中央行に見られる強い全体信号は大小様々な強度の成分信号から成り立っており、、外側に行くほどみられる全体信号は弱めです。しかも、その程度にはあまり大きな違いがない成分信号から成り立っているといえます。

 

信号強度が大きく違えばそれだけコントラストが大きくなり、その逆の信号強度が小さければコントラストも小さくなります。

 

中央行やその近傍に記録された波形は、情報量が多い強信号から成り立ち、信号強度の明確な違いが含まれています。信号強度の明確な違いは画像コントラストが良好であるということです。

 

これは、つまり中央行に書きこまれたMR信号がコントラストの情報が豊富に含まれていることに繋がります。よって、ｋ空間の中央部ほど高い波形があるということは、それだけ豊富なコントラスト情報が含まれており、画像コントラスト分解能に関係しているといえます。

 

では、画像を評価するうえで欠かせない、空間分解能に関与する因子はｋ空間ではどこに該当するのでしょうか。

 

一応、簡単な復習を挟むと、空間分解能とは画像の先鋭度に影響している因子です。そしてｋ空間では、端に相当する部分が空間分解能に関係しています。

 

これを位相エンコーディング傾斜磁場と強度を変化させて考えたいと思います。

上の図で、上段には傾斜磁場をかけられておらず位相にズレは起こっています。中段には弱い傾斜磁場がかかっており位相は小さなズレが起こっています。さらに、下段は強い傾斜磁場がかかっており、位相にも大きくズレが起こっています。

 

位相が大きくズレているということは、その矢印の向きの違いがひと目でみてわかるほどです。それが大きな識別さによってあらわており、MRでは空間分解能という画像の先鋭度に大きく関わっているのです。

 

ここまでをまとめると、

・ｋ空間中央行

➀弱い位相エンコーディング傾斜磁場によるMR信号である。
➁信号強度が強く、コントラスト分解能に大きく関与している。

・ｋ空間の端

➀強い位相エンコーディング傾斜磁場によるMR信号である。
➁信号強度が弱く、空間分解能に関与している。

 

 

これを実際に、ｋ空間の中心部分と中心部分を抜いたそれぞれで画像を作ってみると以下のようになります。

ｋ空間が全て埋められたものから画像は問題なく、全ての情報が含まれています。

 

一方、ｋ空間データの辺縁部だけを使って作成した場合、高い空間分解能があり（先鋭度が高く、辺縁がくっきりしている）画像になっていますが、その反面、画像コントラストが乏しいものになっています。

 

また、ｋ空間データの中心部だけでを使って作成画像では、コントラスト分解能が高く、組織差がわかりやすいですが、画像全体としてボケたような画像になっています。

スポンサーリンク

ｋ空間からMR画像ができるまで

ｋ空間に埋められたデータからどうやったら画像ができるのか。

 

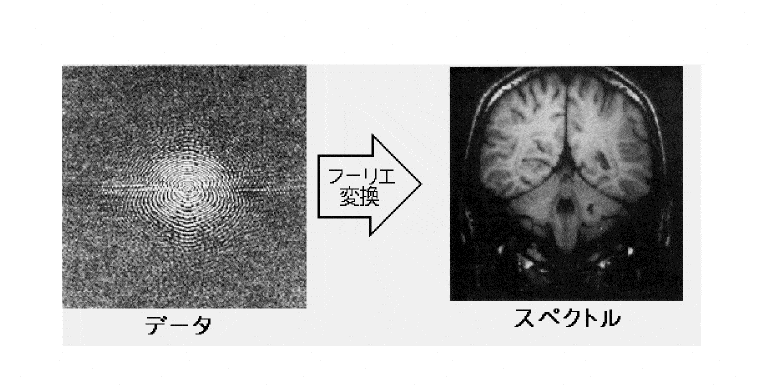
この答えは、フーリエ変換です。

 

フーリエ変換では、複雑な波形を分解し、わかりやすい形に変えることができます。そのフーリエ変換を使って記録波形を要素分解すると、ひとつひとつの全体信号ごとにどのような周波数成分が含まれているのか、定量的な情報を得ることが可能になるのです。

 

周波数方向に並んだそれぞれの点に対して、その周波数成分でどれぐらいの信号強度になっているのかというを数字で表すことが可能です。

 

この分析を行ごとに行うと、強度分布の異なる新たな周波数成分が得られます。これは、強度の異なる位相エンコーディング傾斜磁場を使ったために得られる信号です。

 

実は、フーリエ変換後の信号強度は行の左右方向だけでなく、行が並ぶ縦方向にも変化が見られます。その信号強度変化がどの程度になるかは位相エンコーディング傾斜磁場によって決まるのです。

 

周波数エンコーディング方向では、周波数エンコーディング傾斜磁場の強度に従って信号強度が体系的に影響を受け、位相エンコーディング方向では、位相エンコーディング傾斜磁場によって信号強度は体系的に影響を受けているのです。

 

つまり、周波数エンコーディングにフーリエ変換をすることで横方向のどの地点から信号がでているのか、位相エンコーディング方向にフーリエ変換を行うことで縦方向のどの地点から信号を得たのかというのを知ることが出来ることになります。

 

これによって、信号がどこからでて、どの程度の信号強度が得られているのかというのを解析することができ、MR画像を作ることができるようになるのです。

 

ここまでのことを総合していうと、ｋ空間に保存したMR信号を周波数方向、位相方向とそれぞれフーリエ変換を行うことで、波形は具体的な数値をもった信号となり、最終的に画像を得られることになるのです。